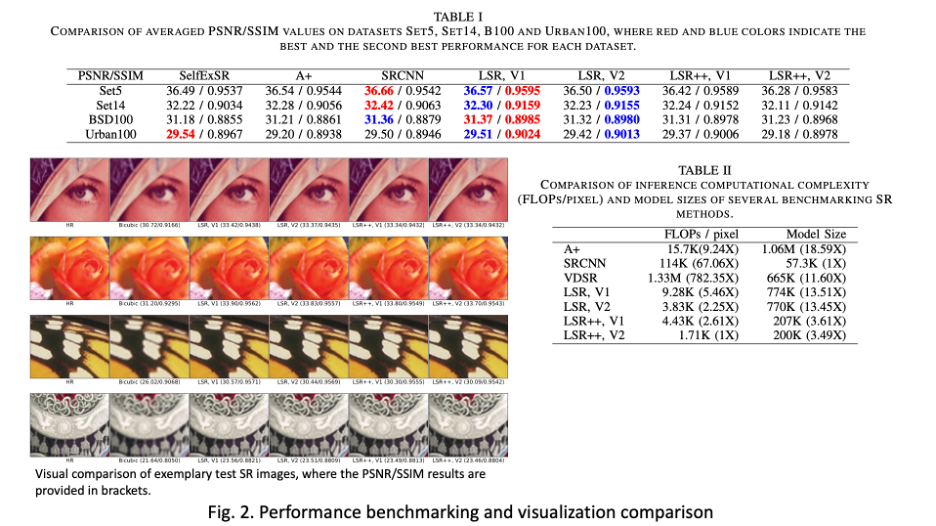
MCL Research on Green Saliency-guided Blind Image Quality Assessment (GSBIQA)
Objective image quality assessment (IQA) is pivotal in various multimedia applications. It can be categorized into three distinct types: Full-Reference IQA (FR-IQA), Reduced-Reference IQA (RR-IQA), and No-Reference IQA (NR-IQA). FR-IQA directly compares a distorted image against a reference or original image to assess quality. RR-IQA, on the other hand, uses partial information from the reference images to evaluate the quality of the target images. NR-IQA, also known as blind image quality assessment (BIQA), becomes essential in scenarios where reference images are unavailable, such as at the receiver’s end or for user-generated content on social media. The demand for BIQA has surged with the increasing popularity of such platforms. BIQA is an essential task that estimates the perceptual quality of images without reference. This field is increasingly relevant due to the rise in user-generated content and mobile applications where reference images are typically unavailable.
The challenge in BIQA lies in the diversity of content and the presence of mixed distortion types. While many BIQA methods employ deep neural networks (DNNs) and incorporate saliency detectors to enhance performance, their large model sizes limit deployment on resource-constrained devices.
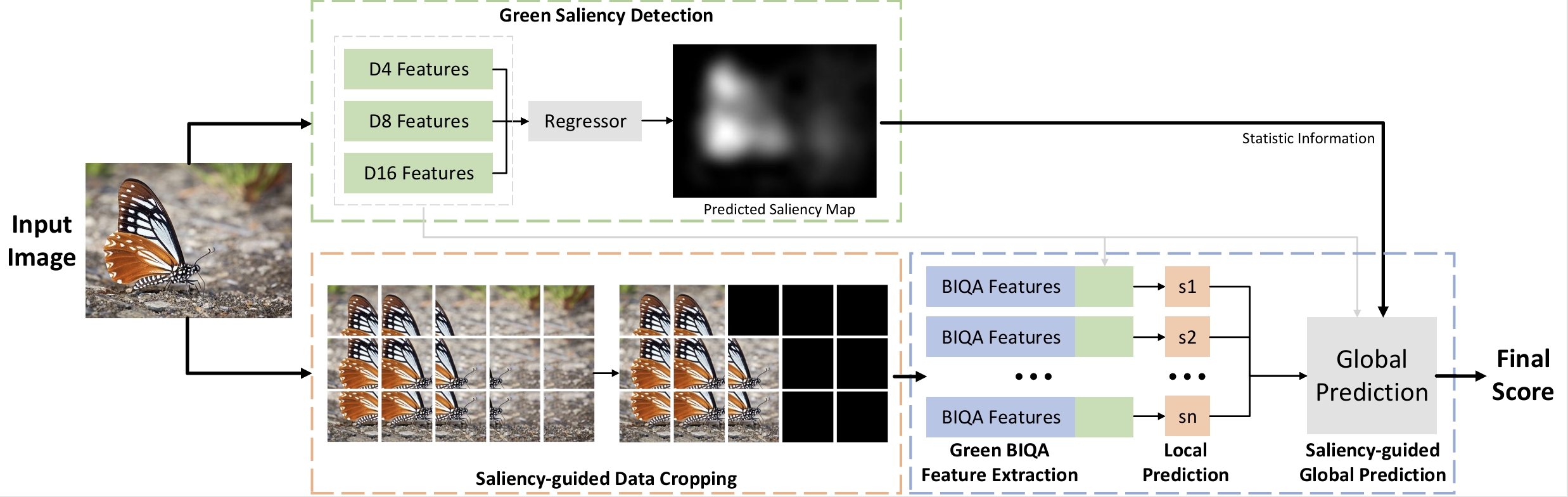
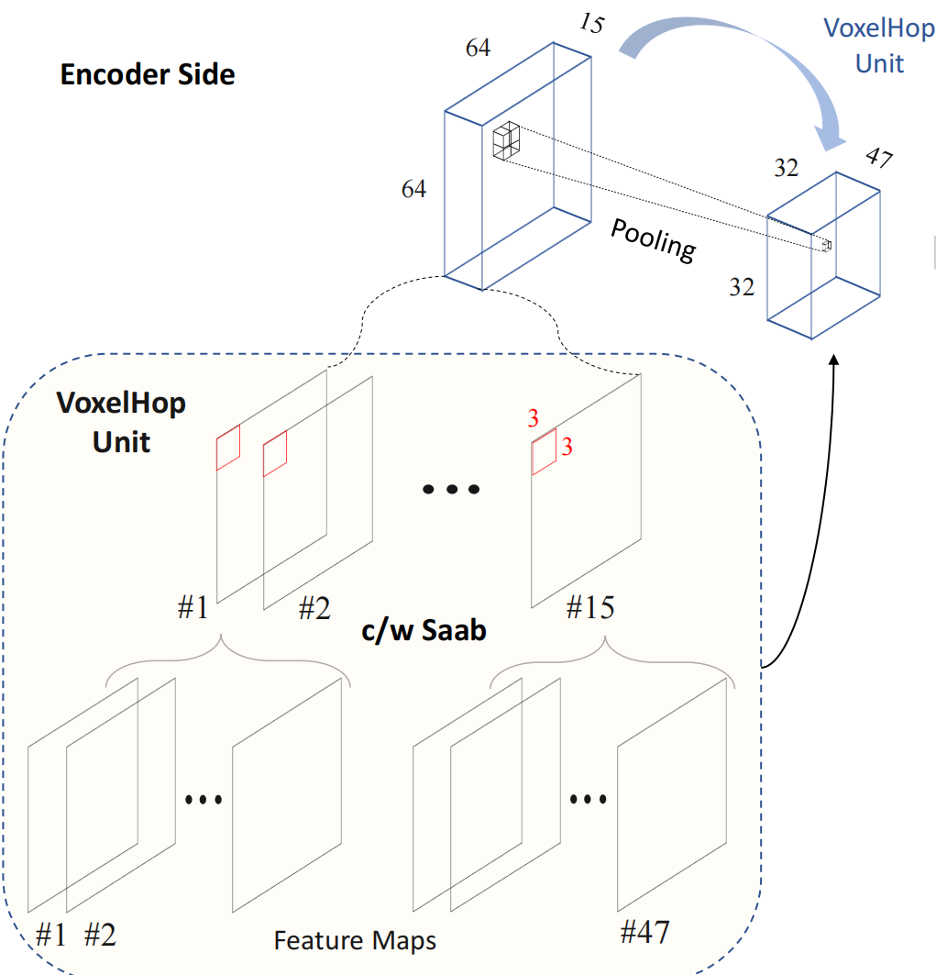
To address this challenge, we introduce a novel and non-deep-learning BIQA method with a lightweight saliency detection module, called Green Saliency-guided Blind Image Quality Assessment (GSBIQA). It is characterized by its minimal model size, reduced computational demands, and robust performance. The lightweight saliency detector in GSBIQA facilitates data cropping and decision ensemble and generates useful features in BIQA that emulate the attention mechanism. The GSBIQA method is structured around five key processes: 1) green saliency detection, 2) saliency-guided data cropping, 3) Green BIQA feature extraction, 4) local patch prediction, and 5) saliency-guided decision ensemble. Experimental results show that the performance of [...]