MCL Research on Green Image Steganalysis
Steganography for spatial images is a technique that involves hiding secret information within digital images in a way that is imperceptible to the human eye. It considers the characteristics and features of the cover media in a local region, and embed the secret information in a manner that is visually or statistically inconspicuous.
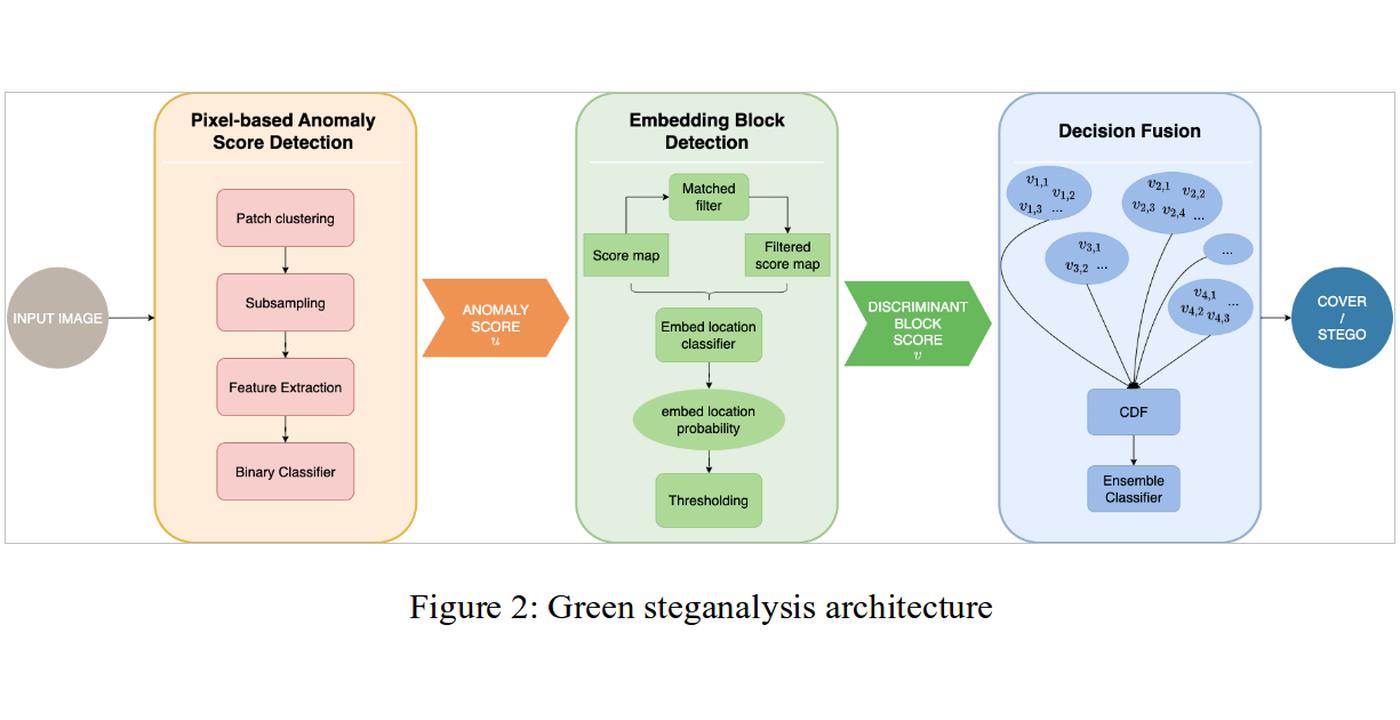
As the other side of the coin, steganalysis, is the way of detecting the embedded image (often we call it stego image). There has been numerous works in detecting the hidden information. Traditionally, people use heuristic features and ensemble of machine learning models for detection. It soon becomes feeble in detecting content adaptive steganographic images. After the emerging of neural networks, researchers start to use deep models to detect the weak stego signals by extracting features and doing classification in a whole. Different from the traditional steganalysis and deep learning based steganalysis methods, we propose a novel steganalysis scheme, which is a green steganalysis method.
We first scatter the whole image into small blocks, and then perform anomaly detection on block levels. This step will give us an indication of the likelihood such that this block is embedded or not. Next, we train an embed location detector, to help us locate the blocks that are more discriminant than others. Finally, blocks that are selected from previous step will be fused together and make image-level decision by ensemble classifier. Our architecture is completely explainable, and computationally efficient.
— by Yao Zhu