MCL Research on Mice Navigation Pattern Strategies
Understanding how animals navigate and learn from their environments has long been a central question in neuroscience. The Morris Water Maze (MWM) is one of the most widely used paradigms for studying spatial learning and memory in rodents. Traditionally, researchers have assessed performance using simple metrics such as escape latency and total path length. While these measures quantify task efficiency, they fail to capture the diversity of navigation strategies that rodents employ within a single trial. Recent work has revealed that mice often transition dynamically between different behavioral modes, such as thigmotaxis, scanning target, and direct search, suggesting that whole-trajectory analyses may overlook important within-trial strategy shifts.
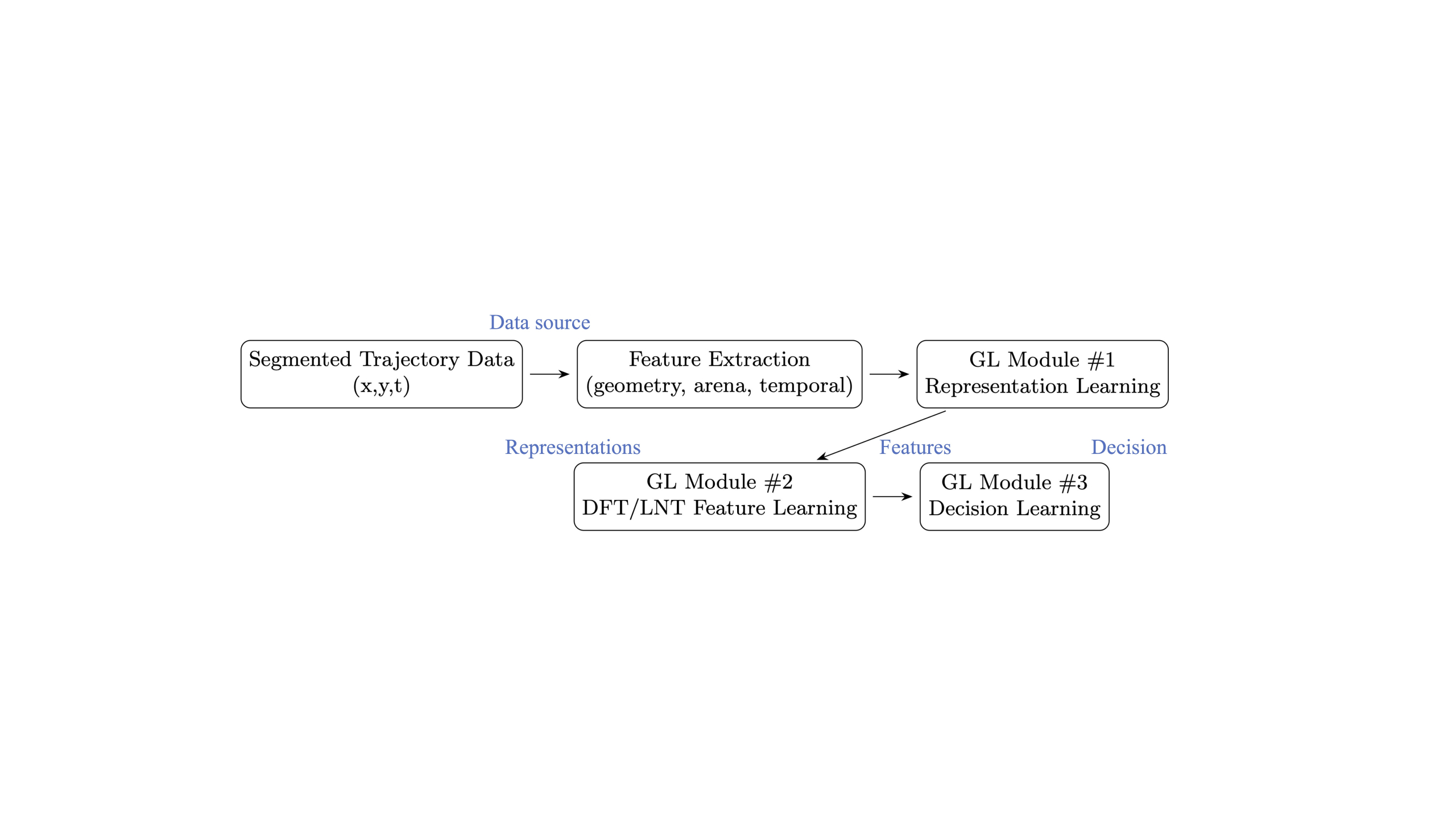
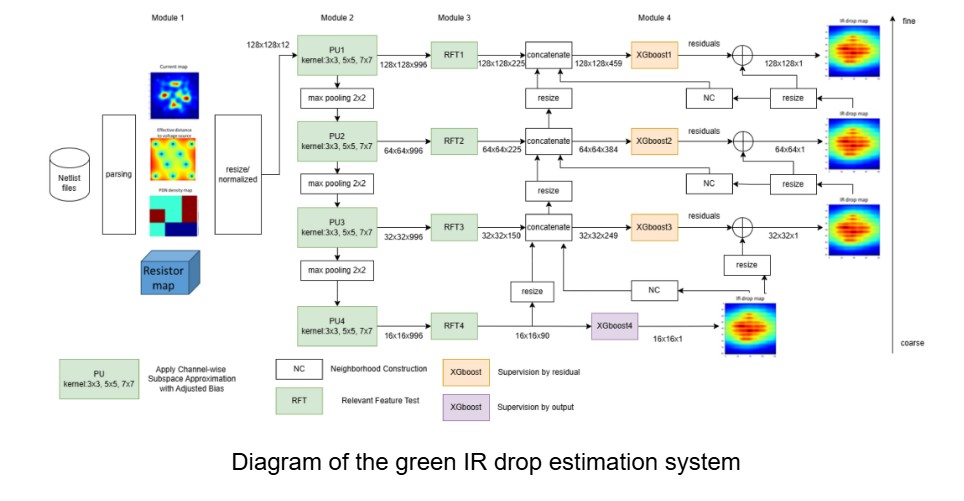
To address this, we develop a Green Learning (GL) based framework to classify sub-trajectories into expert-defined behavioral strategies in an energy-efficient and interpretable manner. Unlike deep learning methods that depend on large datasets, backpropagation, and heavy computation, GL employs a feedforward-designed architecture emphasizing energy efficiency, logical transparency, and interpretability.
Our framework integrates trajectory segmentation with the three modules of GL, representation learning, feature learning, and supervised decision making. The segmentation stage divides each swimming path into overlapping sub-trajectories, allowing fine-grained behavioral classification rather than treating the entire trial as a single unit. We then extract geometric and temporal features, which serve as inputs for representation learning. Subsequently, Discriminant Feature Test (DFT) and Least-squares Normal Transform (LNT) modules identify the most informative and interpretable features for distinguishing strategies. Finally, Subspace Learning Machines (SLM) and ensemble classifiers perform supervised decision learning with minimal computational cost.
Through this interpretable and sustainable approach, we aim to uncover subtle behavioral differences between experimental and control groups while reducing energy consumption and improving transparency in AI-driven behavioral analysis. The proposed framework not only advances rodent behavioral [...]