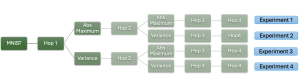
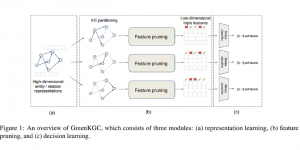
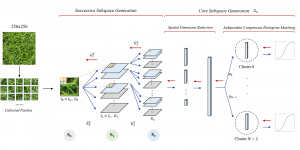
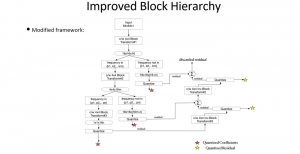
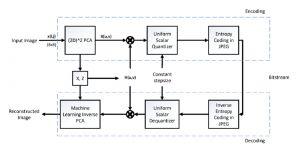
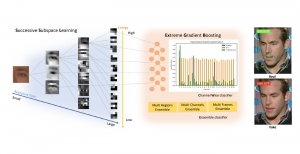
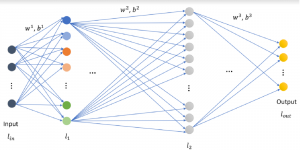
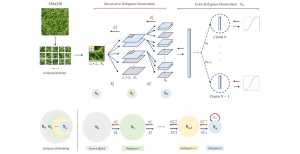
An image generative model learns the distribution of image samples from a certain domain and then generates new images that follow the learned distribution. The design of image generative models involves analysis and generation two pipelines. The former analyzes properties of training image samples while the latter generates new images after the training is completed. Only the generation unit is used for image generation in inference. There is a resurge of interests in generative models due to the amazing performance achieved by deep-learning-based (DL-based) methods in general and generative adversarial networks (GANs) in particular. Yet, DL-based methods attempt to solve a nonconvex optimization problem which is difficult to explain. GAN’s training may suffer from gradient vanishing, convergence difficulty and mode collapse. Furthermore, its implementation demands higher computational resources due to large model sizes.
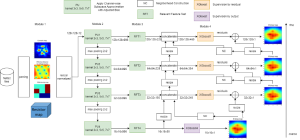
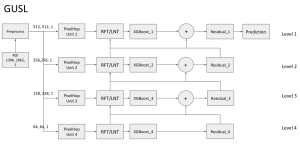
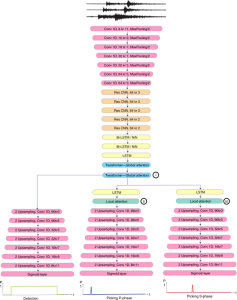
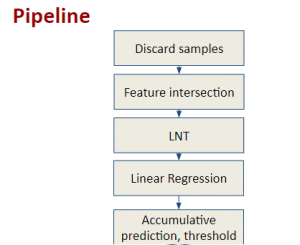
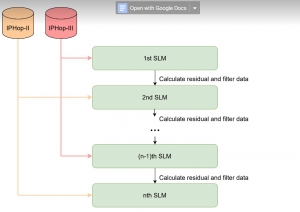
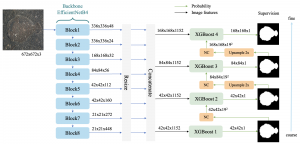
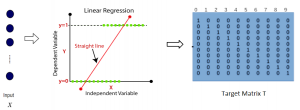
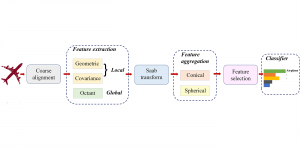
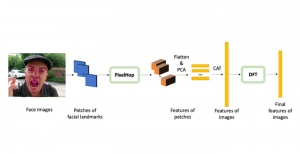
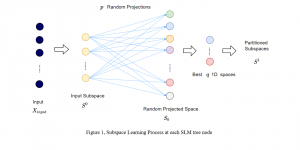
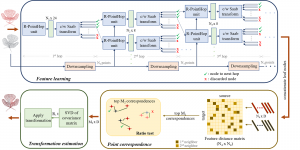
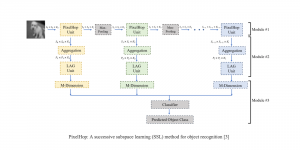
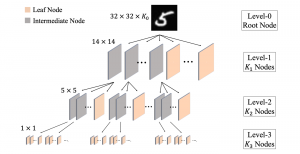
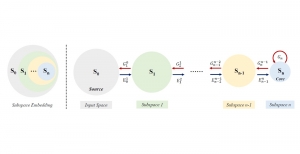
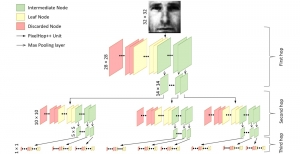
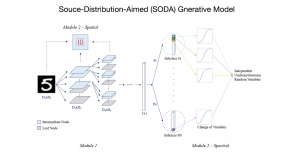
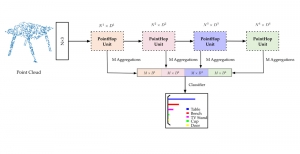
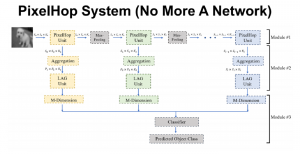
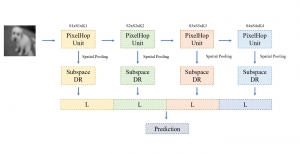
The design of GANs demands that distributions of training and generated images be indistinguishable, which is implicitly achieved by training a generator/discriminator pair through end-to-end optimization of a cost function. In contrast with the GAN approach, we propose a novel and explainable image generation method with explicit sample distribution modeling in this work. For image analysis, we construct fine-to-coarse spatial-spectral subspaces using the PixelHop++ architecture and obtain sample distributions in each subspace. For image generation, we reverse the process by generating samples in the coarsest subspace and add more details to these samples gradually. Our solution, called GenHop (an acronym of Generative Pixelhop), offers an unconditional generative model. Based on MNIST and Fashion-MNIST two datasets, GenHop can generate visually pleasant images whose FID scores are comparable with those of DL-based generative models.