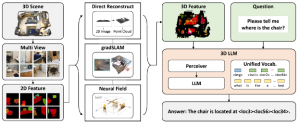
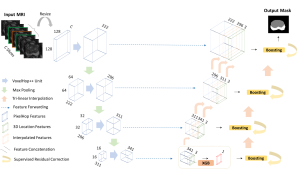
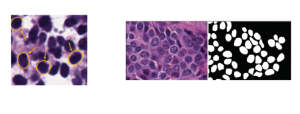
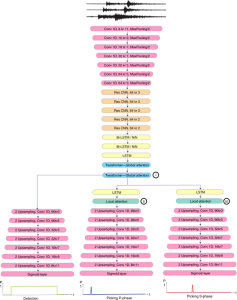
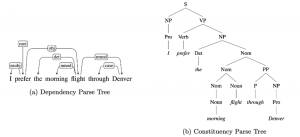
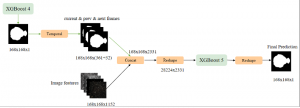
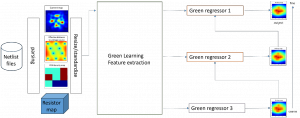
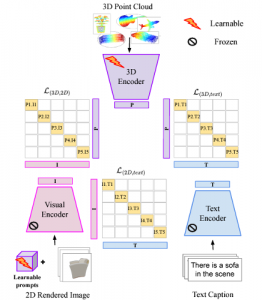
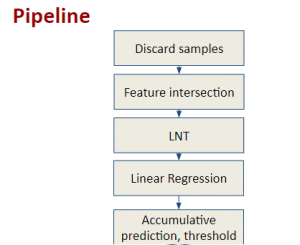
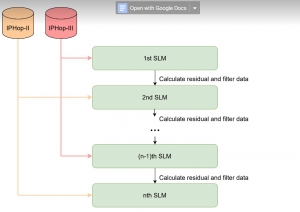
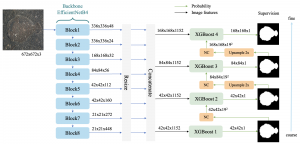
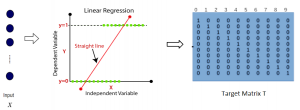
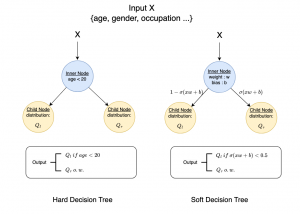
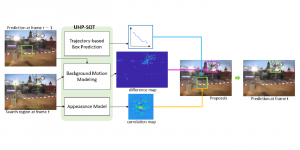
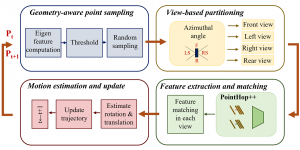
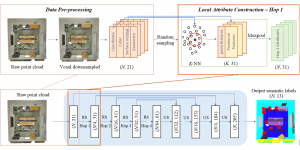
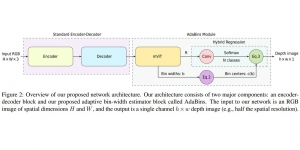
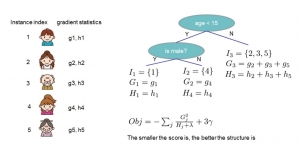
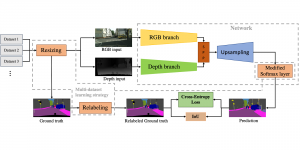
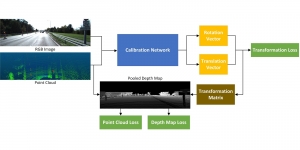
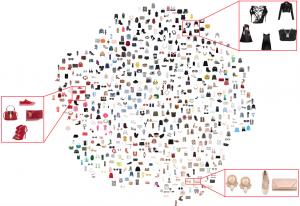
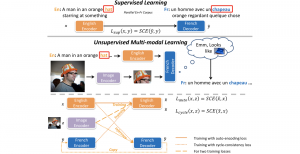
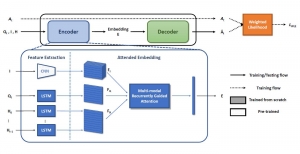
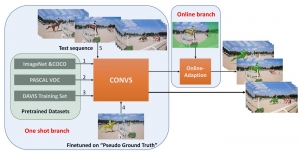
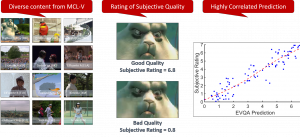
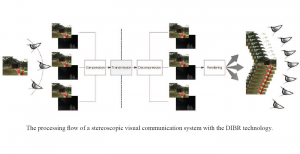
There are typically two types of statistical models in mechine learning, discriminative models and generative models. Different from discriminative models that aim at drawing decision boundaries, generative models target at modeling the data distribution in the whole space. Generative models tackle a more difficult task than discriminative model because it needs to model complicated distributions. For example, generative models should capture correlations such as “Things look like boats are likely to appear near things that look like water” while discriminative model differentiates “boat” from “not boat”.
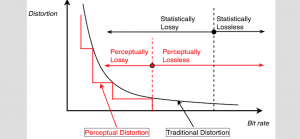
Image generative models have become popular in recent years since Generative Adversarial Network (GANs), can generate realistic natural images. They, however, have no clear relationship to probability distributions and suffer from difficult training process and mode dropping problem. Although difficult training process and mode dropping problems may be alleviated by using different loss functions [1], the underlying relationship to probability distributions remains vague in GANs. It encourages us to develop a SOurce-Distribution-Aimed (SODA) generative model that aims at providing clear probability distribution functions to describe data distribution.
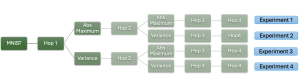
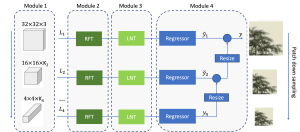
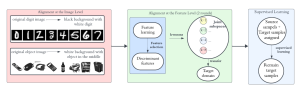
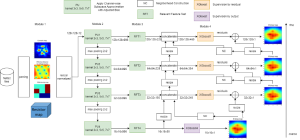
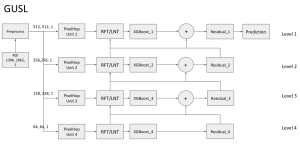
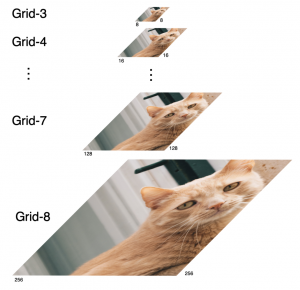
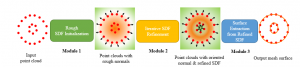
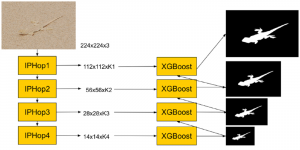
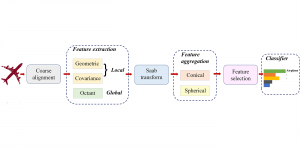
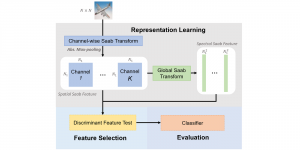
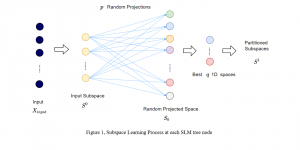
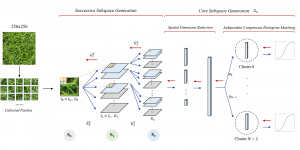
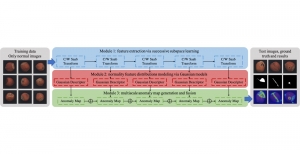
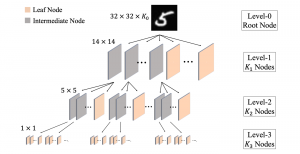
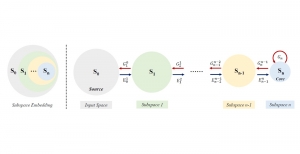
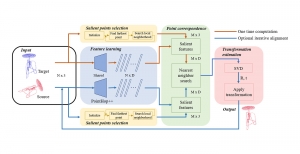
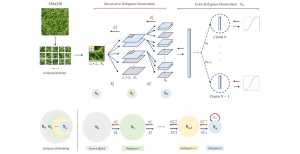
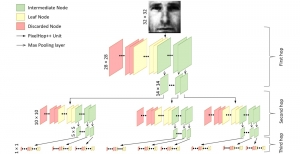
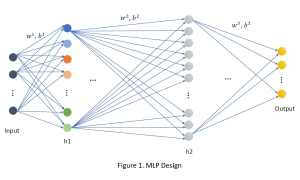
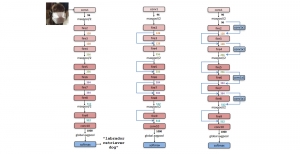
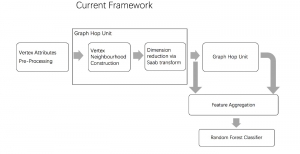
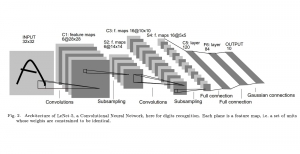
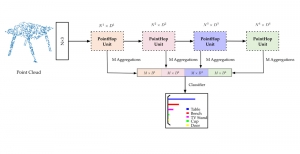
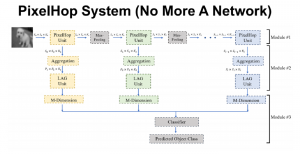
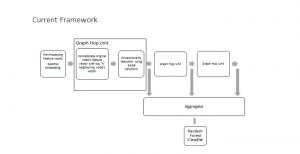
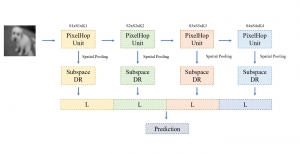
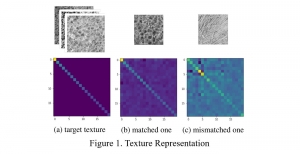
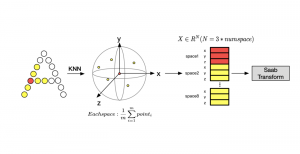
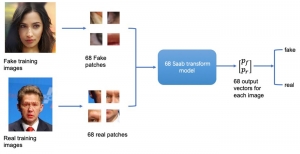
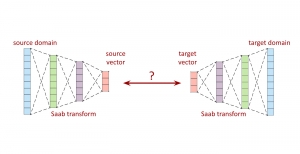
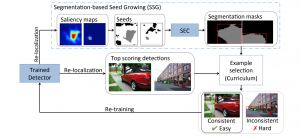
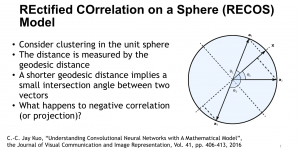
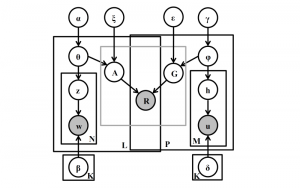
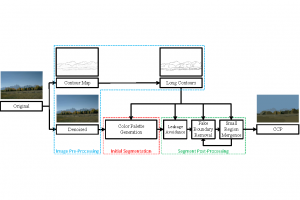
There are two main modules in our SODA generative model. One is finding proper source data representations and the other is determining the source data distribution in each representation. One proper representation for source data is joint spatial-spectral representation proposed by Kuo, et.al. [2, 3]. By transforming between spectral domain and spatial domain, a rich set of spectral and spatial representations can be obtained. Spectral representations are vectors of Saab coefficients while spatial representations are pixels in an image or Saab coefficients that are arranged based on their pixel order in spatial domain. Spectral representation at the last stage give a global view of an image while the spatial representations describe details in the local area of the image. In this case, our SODA generative model can learn global spectral distribution of the source data as well as local spatial distribution. To determine global spectral distribution, we partition the whole space into several subspaces and find the distributions of a set of independent random variables in each subspace. This is inspired by divide and conquer algorithm, which recursively breaking down a problem into two or more sub-problems with related type until each subproblem becomes simple enough to be solved directly. To determine local spatial distribution, we model the condition probability of local area of source data given the global data distribution and generate offset maps for spatial representations. By looking at images globally and locally, our SODA generative model can synthesize realistic and natural images with high diversity and fidelity.
— By Xuejing Lei
References:
[1] Lucic, Mario, et al. “Are gans created equal? a large-scale study.” Advances in neural information processing systems. 2018.
[2] Kuo, C-C. Jay, et al. “Interpretable convolutional neural networks via feedforward design.” Journal of Visual Communication and Image Representation 60 (2019): 346-359.
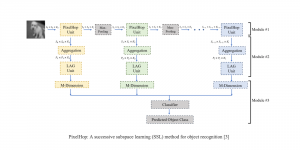
[3] Chen, Yueru, et al. “PixelHop++: A Small Successive-Subspace-Learning-Based (SSL-based) Model for Image Classification.” arXiv preprint arXiv:2002.03141 (2020).