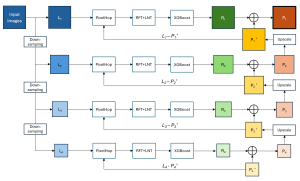
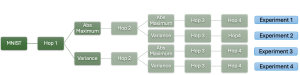
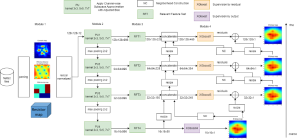
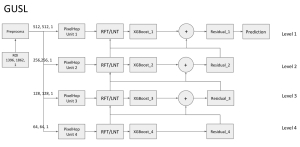
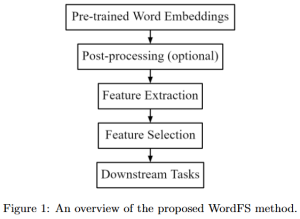
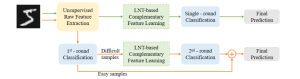
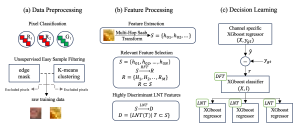
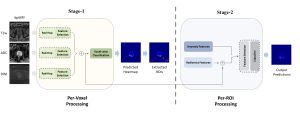
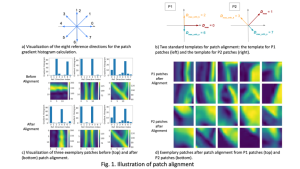
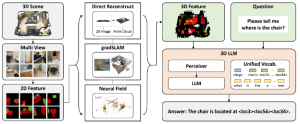
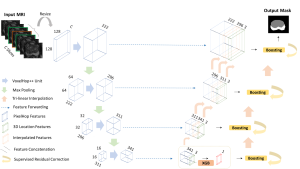
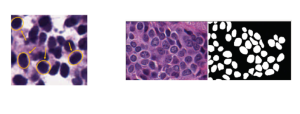
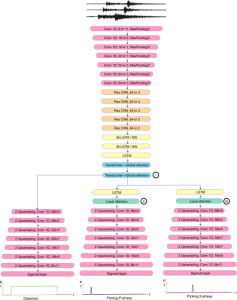
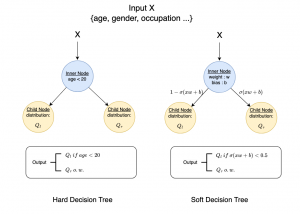
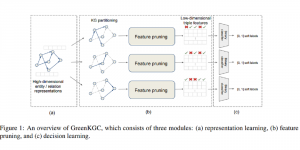
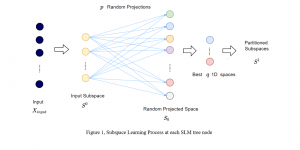
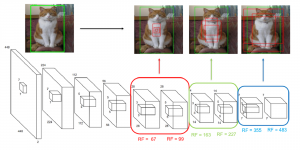
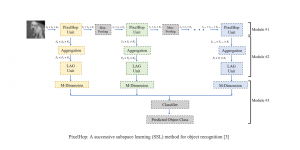
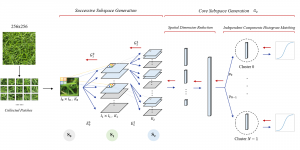
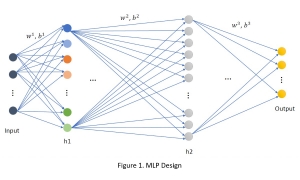
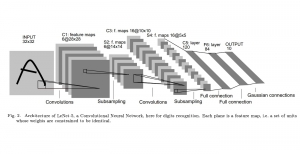
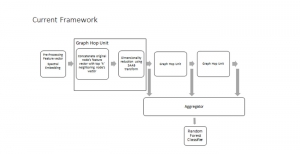
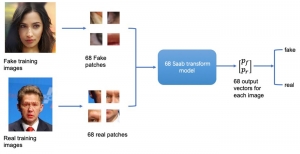
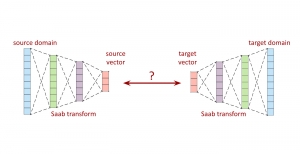
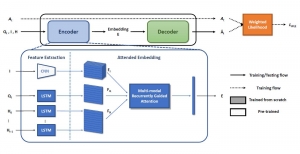
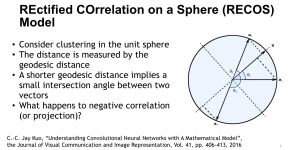
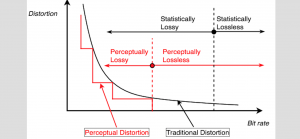
It is well known that CNNs-based methods have weaknesses in terms of efficiency, scalability, and robustness. CNNs-based methods require large computational efforts and are not scalable to the change of object class numbers and the dataset size. Furthermore, these CNN models are not robust to small perturbations due to their excess dependence on the end-to-end optimization methodology. The Saak (Subspace approximation with augmented kernels) transform [1] is proposed to provide the possible solution to overcome these shortcomings.

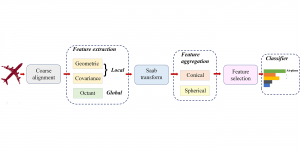
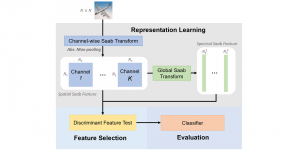
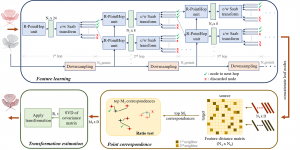
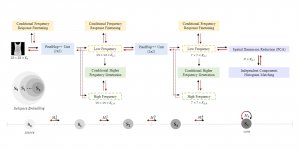
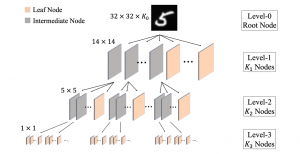
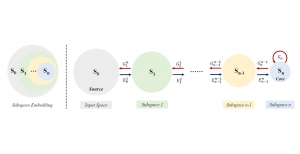
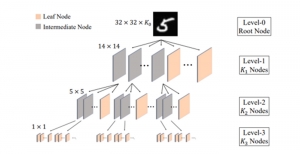
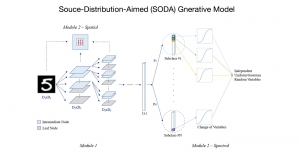
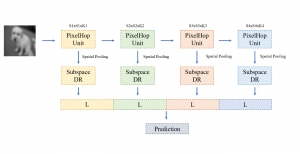
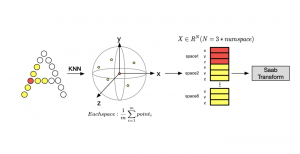
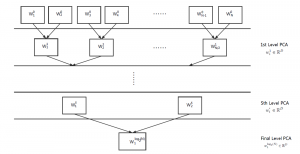
The Saak transform consists of two new ingredients on top of traditional CNNs. They are: subspace approximation and kernel augmentation. The Saak transform allows both forward and inverse transforms so that it can be used for image analysis as well as synthesis (or generation). One can derive a family of joint spatial-spectral representations between two extremes – the full spatial-domain representation and the full spectral-domain representation using multi-stage Saak transforms. Being different with CNNs, all transform kernels in multi-stage Saak transforms are computed by one-pass feedforward process. Neither data labels nor backpropagation is needed for kernel computation.

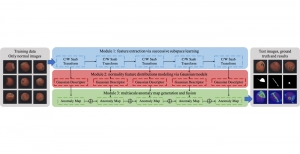
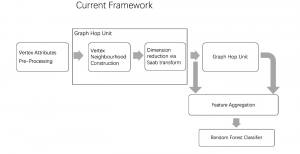
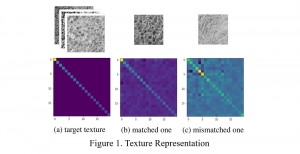
Currently, we have successfully developed Saak transform approaches [2] to solve the handwritten digits recognition problem. This new approach has several advantages such as higher efficiency than the lossless Saak transform, scalability against the variation of training data size and object class numbers and robustness against noisy images. In the near future, we would like to apply the Saak transform approach to the general object classification problem with more challenging datasets such as CIFAR-10, CIFAR-100, and ImageNet.

Reference

[1]  C-C Jay Kuo and Yueru Chen, “On Data-driven Saak Transform,” arXiv preprint arXiv:1710.04176, 2017.

[2] Chen, Y., Xu, Z., Cai, S., Lang, Y., & Kuo, C. C. J. (2017). A Saak Transform Approach to Efficient, Scalable and Robust Handwritten Digits Recognition. arXiv preprint arXiv:1710.10714.

By Yueru Chen