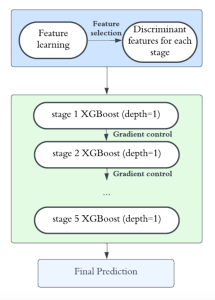
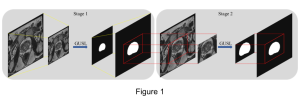
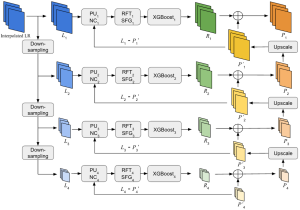
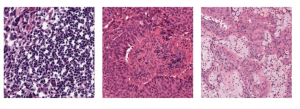
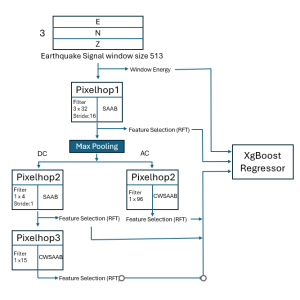
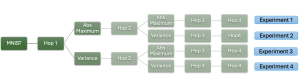
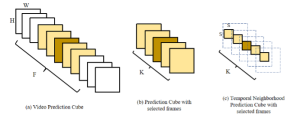
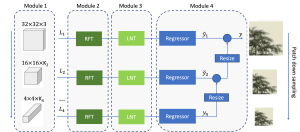
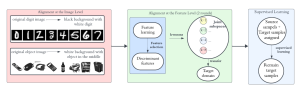
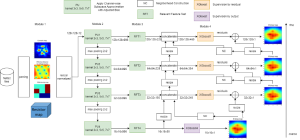
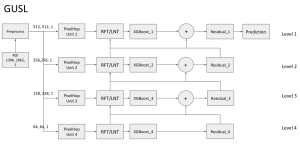
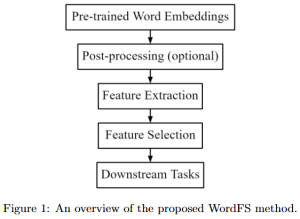
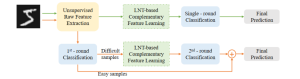
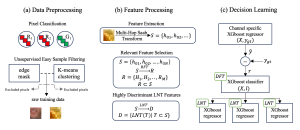
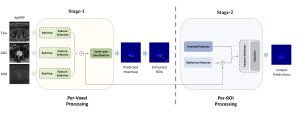
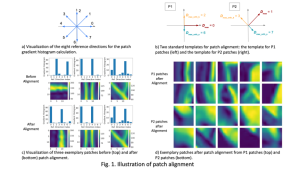
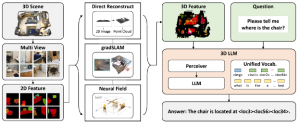
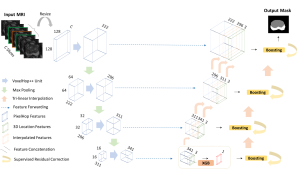
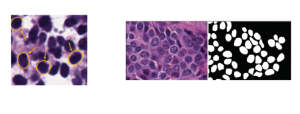
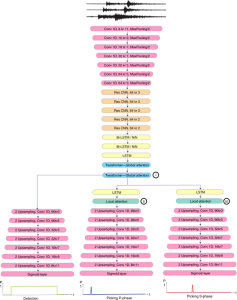
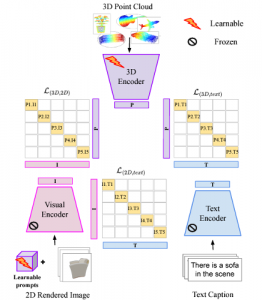
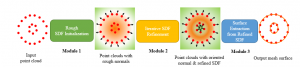
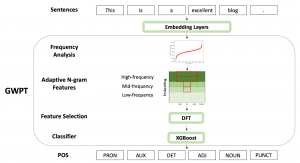
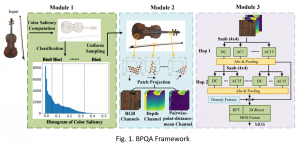
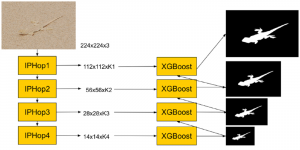
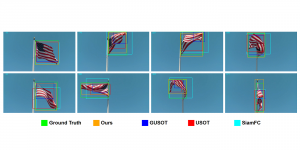
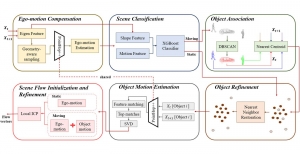
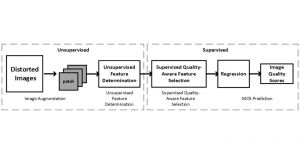
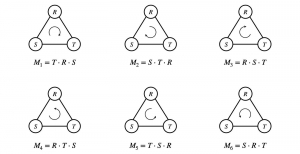
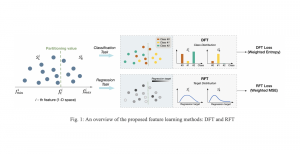
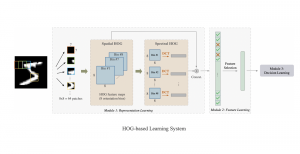
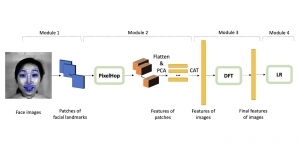
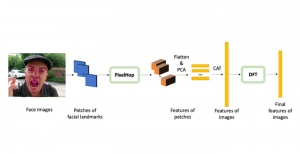
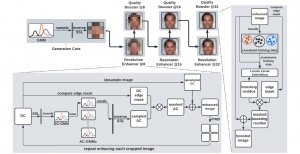
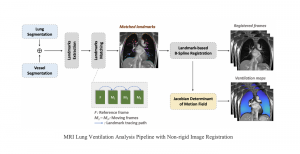
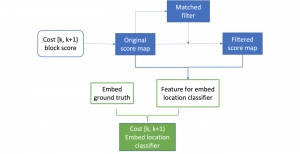
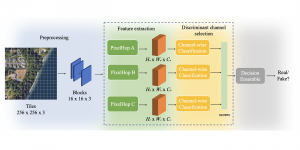
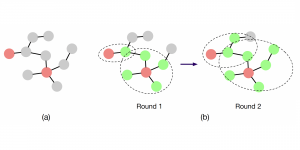
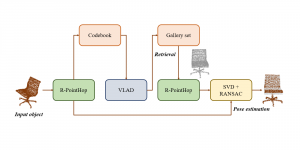
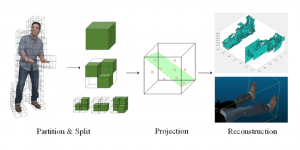
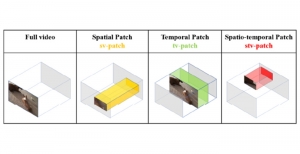
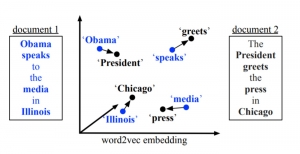
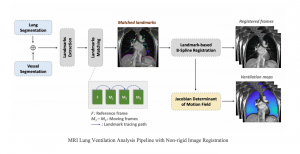
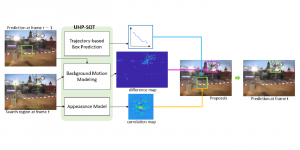
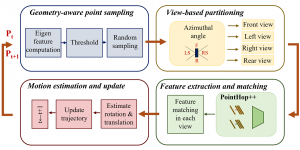
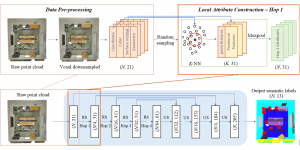
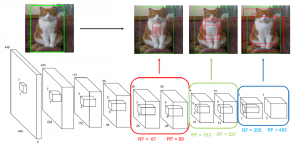
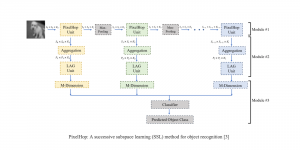
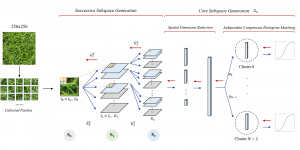
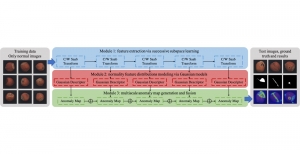
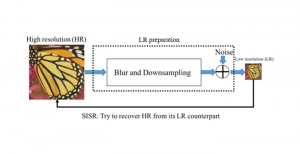
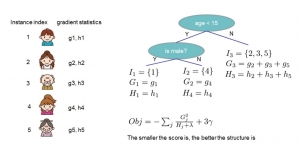
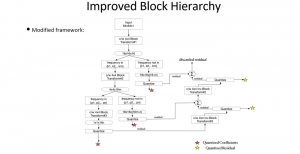
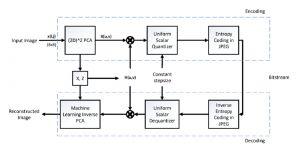
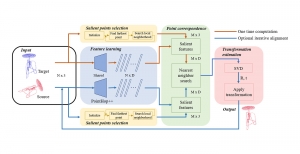
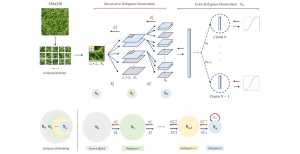
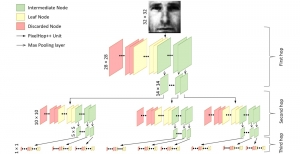
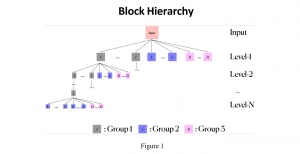
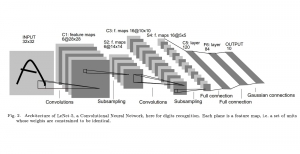
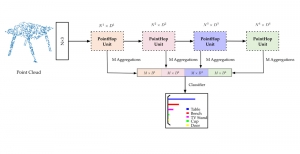
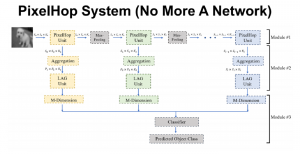
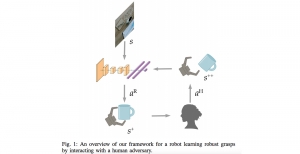
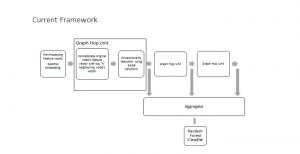
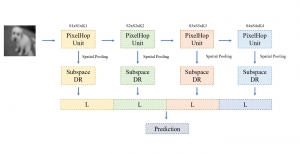
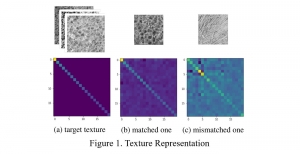
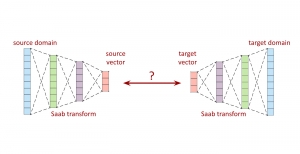
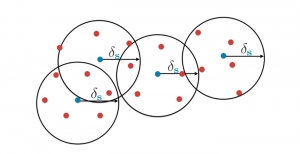
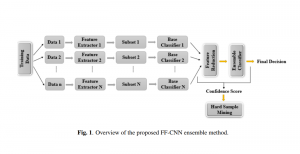
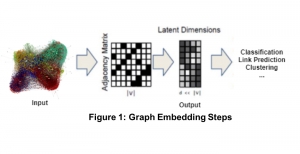
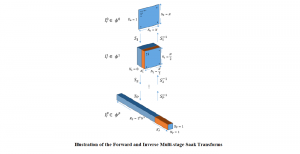
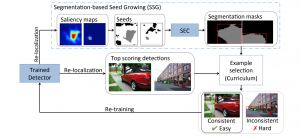
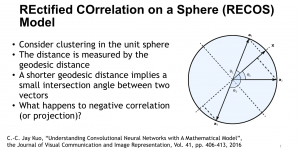
Our work on new MLP interpretation includes:
- Interpretable MLP design [1]:
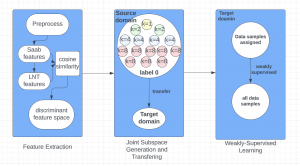
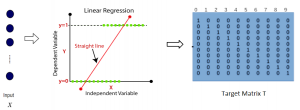
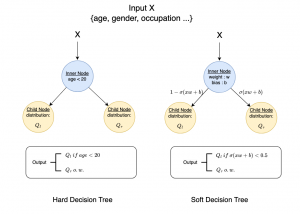
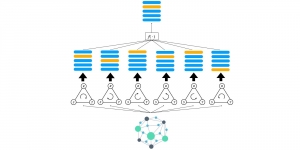
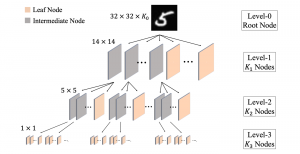
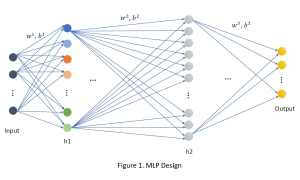
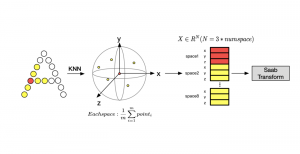
A closed-form solution exists in two-class linear discriminant analysis (LDA), which discriminates two Gaussian-distributed classes in a multi-dimensional feature space. In this work, we interpret the multilayer perceptron (MLP) as a generalization of a two-class LDA system so that it can handle an input composed by multiple Gaussian modalities belonging to multiple classes. Besides input layer lin and output layer lout, the MLP of interest consists of two intermediate layers, l1 and l2. We propose a feedforward design that has three stages: 1) from lin to l1: half-space partitionings accomplished by multiple parallel LDAs, 2) from l1 to l2: subspace isolation where one Gaussian modality is represented by one neuron, 3) from l2 to lout: class-wise subspace mergence, where each Gaussian modality is connected to its target class. Through this process, we present an automatic MLP design that can specify the network architecture (i.e., the layer number and the neuron number at a layer) and all filter weights in a feedforward one-pass fashion. This design can be generalized to an arbitrary distribution by leveraging the Gaussian mixture model (GMM). Experiments are conducted to compare the performance of the traditional backpropagation-based MLP (BP-MLP) and the new feedforward MLP (FF-MLP).
- MLP as a piecewise low-order polynomial approximator [2]:
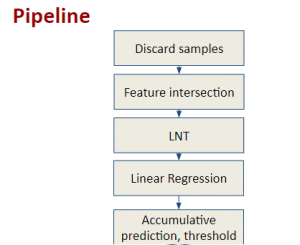
The construction of a multilayer perceptron (MLP) as a piecewise low-order polynomial approximator using a signal processing approach is presented in this work. The constructed MLP contains one input, one intermediate and one output layers. Its construction includes the specification of neuron numbers and all filter weights. Through the construction, a one-to-one correspondence between the approximation of an MLP and that of a piecewise low-order polynomial is established. Comparison between piecewise polynomial and MLP approximations is made. Since the approximation capability of piecewise low-order polynomials is well understood, our findings shed light on the universal approximation capability of an MLP.
[1] R. Lin, Z. Zhou, S. You, R. Rao, and C.-C. J. Kuo, “From two-class linear discriminant analysis to interpretable multilayer perceptron design,” arXiv preprint arXiv:2009.04442, 2020.
[2] R. Lin, S. You, R. Rao, and C.-C. J. Kuo, “Constructing multilayer perceptrons as piecewise low-order polynomial approximators: A signal processing approach,” arXiv preprint arXiv:2010.07871, 2020.