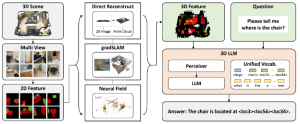
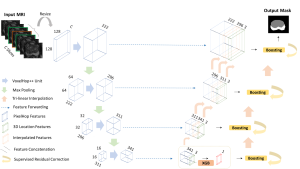
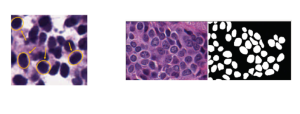
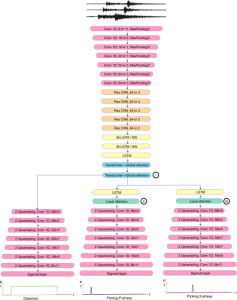
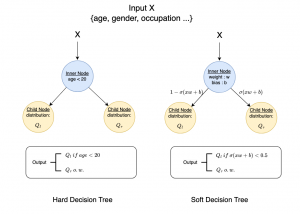
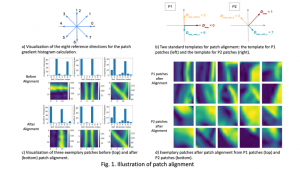
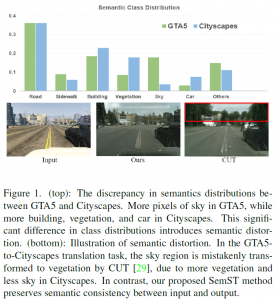
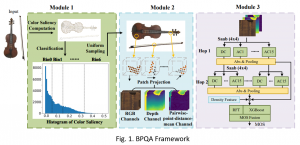
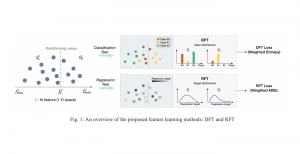
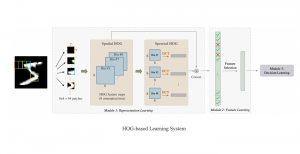
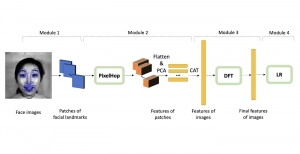
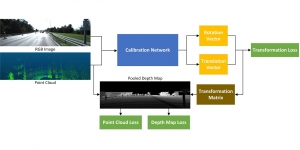
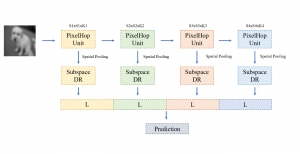
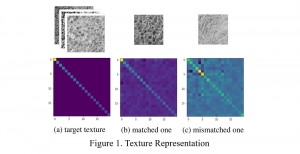
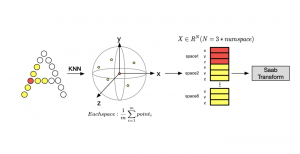
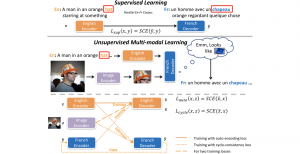
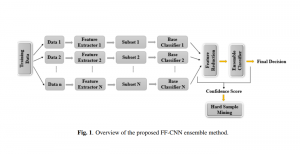
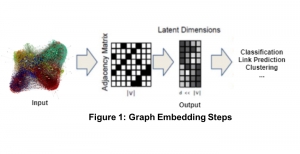
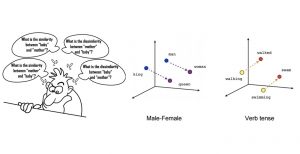
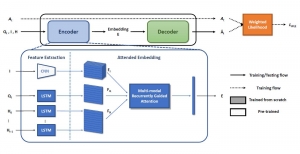
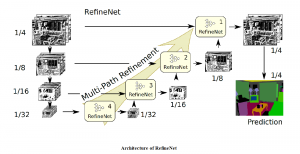
In the MCL genealogy, Carl Friedrich Gauss is a shining star. Min Zhang studied his unusual life and shared with MCL members in the pre-seminar sharing on October 03, 2022. Gauss is the greatest mathematician since antiquity, known for his contributions to number theory, proving the fundamental theorem of algebra, deriving the function representation of normal distribution, his contribution to the theory of magnetism and being PhD advisor to Richard Dedekind and Bernhard Riemann.
Carl Friedrich Gauss was born on April 30, 1777, in Brunswick in the Duchy of Brunswick-Wolfenbüttel which now part of Lower Saxony, Germany. His parents were poor, working-class citizens. His mother was illiterate and never recorded his birthdate, remembering only that was a Wednesday, eight days before the Feast of the Ascension. Gauss figured out his birthday by deriving the date of Easter by himself. There are some interesting anecdotes about Gauss when he was a child. Gauss is child prodigy, he was said to have corrected an error in this father’s payroll calculations at the age of 3, he dazzled his schoolteachers by quickly summing up the integers from 1 to 100 to be 5050 at the age of 7 and he was already criticizing Euclid’s geometry at the age of 12.
Gauss’s intellectual abilities attracted the attention of the Duke of Brunswick, the Duke supported his study and life since he was 14 years old until the Duke passed away in 1806. With the funding from the Duke, Gauss studied at the Collegium Carolinum (now Braunschweig University of Technology) from 1792 to 1795. Then, he got a bachelor’s degree at the University of Göttingen in 1798 when he was 22. Gauss was very productive in 1796. He advanced modular arithmetic and developed Gauss’s law of quadratic reciprocity which allows mathematicians to determine the solvability of any quadratic equation in modular arithmetic. He constructed heptadecagon, a 17-sided polygon, which was a breakthrough over 2000 years, and found a regular polygon can be constructed with compass and straightedge if and only if the number of sides is the product of a power of 2 and any number of distinct Fermat primes. This construction discovery firmly turned Gauss towards a career of mathematics instead of studying language. Gauss wrote his first book, Disquisitiones Arithmeticae, in 1798 and officially published it in 1801 when he was 24. This book is a fundamental work in number theory. In 1799, Gauss got his PhD degree from the University of Helmstedt, supervised by Johann Fredrich Pfaff. His doctoral thesis gave the first proper proof of the fundamental theorem of algebra formulated over the real line.
Gauss used his mathematical skills to help rediscover a dwarf planet Ceres in December 1801. Benefited from this contribution, he was appointed Professor of Astronomy and Director of the astronomical observatory at the University of Göttingen in 1807, a post he held for the remainder of his life. Moreover, the discovery of Ceres led Gauss to his work on a theory of motion of the celestial bodies moving in conic sections around the Sun, eventually published in 1809. In the book, Gauss discussed differential equations, conic sections, elliptic sections and how to estimate and refine estimation of a planet’s orbit. In the 1920s, Gauss did a geodetic survey of the Kingdom of Hanover, linking up with previous Danish surveys. To aid the survey, Gauss invented the heliotrope, an instrument that uses a mirror to reflect sunlight over great distances, to measure positions. In the 1930s, Gauss collaborated with Wilhelm Weber on a measurement of the Earth’s magnetic field, leading to new knowledge in magnetism (including finding a representation for the unit of magnetism in terms of mass, charge, and time) and the discovery of Kirchhoff’s circuit laws in electricity. It was during this time that he formulated his namesake law.
On 23 February 1855, Gauss died of a heart attack in Göttingen, aged 77. To memorize him, from 1989 through 2001, Gauss’s portrait, a normal distribution curve and some prominent Göttingen buildings were featured on the German ten-mark banknote. Germany has also issued three postage stamps honoring Gauss. The International Mathematics Union (IMU) and the German Mathematical Society jointly launched an awarded in his honor every four years since 2006, including a medal and a cash purse of $14000. This award is for outstanding mathematical contributions that have found significant applications outside of mathematics.
It is not knowledge, but the act of learning, not possession but the act of getting there, which grants the greatest enjoyment. ——Gauss
Reference
- https://en.wikipedia.org/wiki/Carl_Friedrich_Gauss
- https://www.youtube.com/watch?v=Pqh9CK7wBZo
- https://en.wikipedia.org/wiki/Gauss%27s_law