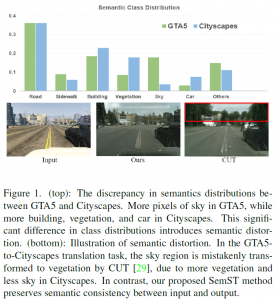
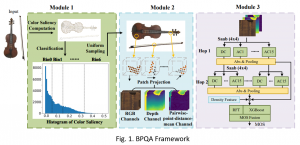
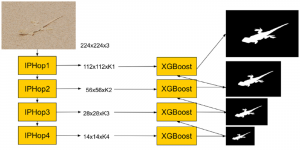
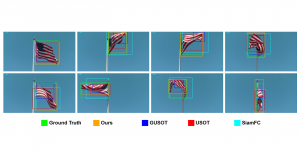
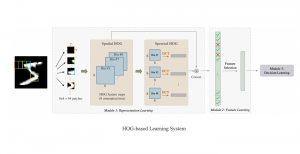
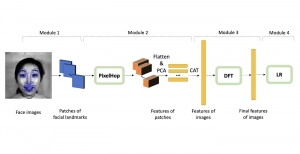
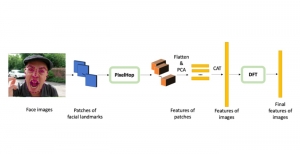
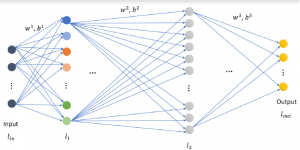
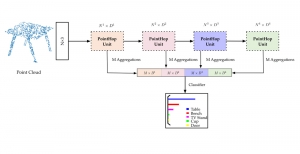
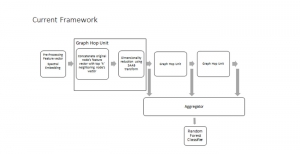
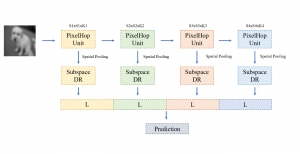
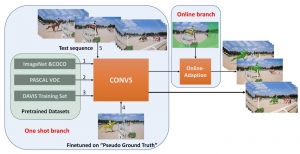
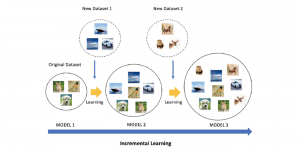
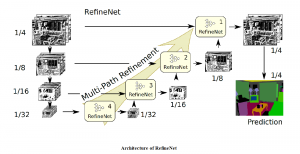
Convolutional neural networks (CNNs) have received a lot of attention in recent years due to their superior performance in computer vision benchmarking datasets. Yet, little theory has been developed to explain the underlying principle of CNNs.

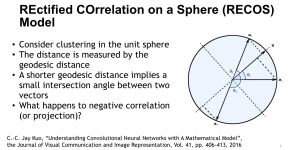
Professor C.-C. Jay Kuo, Director of the Media Communication Lab, has recently published important theoretical results about two CNN fundamental properties. They are: 1) why a non-linear activation function is essential at the filter output of every intermediate layer? and 2) what is the advantage of the two-layer cascade system over the one-layer system? To answer these two questions, he developed a mathematical model called the “REctified-COrrelations on a Sphere” (RECOS).

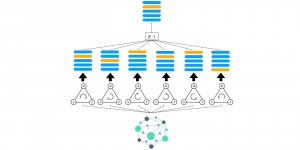
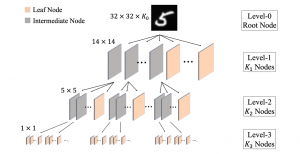
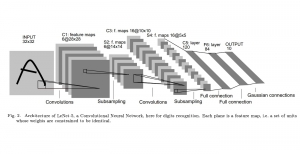
Professor Kuo said, “CNNs need to store the knowledge learned from a large amount training data somewhere. The only places to store the knowledge are the converged filter weights. They must play a critical role in CNN understanding.” Professor Kuo coined a new term “anchor vectors” for the converged filter weights since they serve as a set of vectors for an arbitrary input vector to project onto at one layer. The projected values are the response from the previous layer while their rectified values serve as the input to the next layer. In his paper entitled with “Understanding Convolutional Neural Networks with A Mathematical Model”, Professor Kuo used the anchor vector concept to explain the necessity of nonlinear activation, analyze the behavior of a two-layer RECOS system, and compare it with its one-layer counterpart. He used the LeNet-5 applied to the MNIST dataset as an illustration example throughout the paper.

Professor Kuo emphasized that the new “anchor vector” viewpoint will lead to more interesting research in the near future. His paper has recently been accepted for publication in the Journal of Visual Communication and Image Representation. An earlier version of this work was translated to Chinese. Congratulations to Professor Kuo!