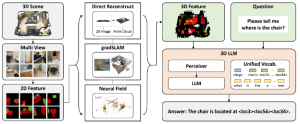
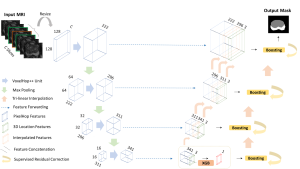
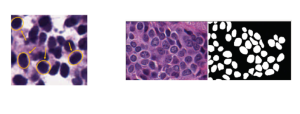
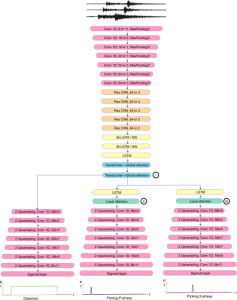
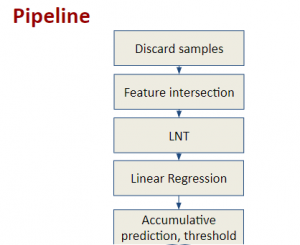
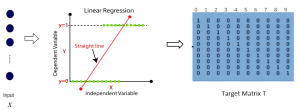
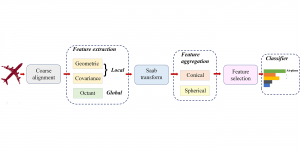
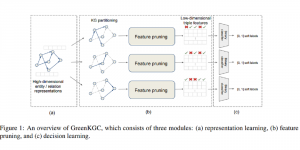
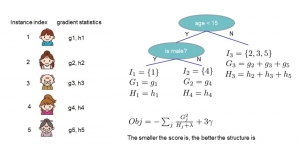
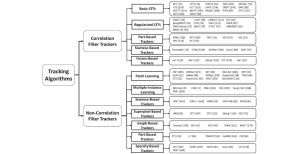
Subspace methods have been widely used in signal/image processing, pattern recognition, computer vision, etc.   One may use a subspace to denote the feature space of a certain object class, (e.g., the subspace of the dog object class) or the dominant feature space by dropping less important features (e.g., the subspace obtained via principal component analysis or PCA). The subspace representation offers a powerful tool for signal analysis, modeling and processing. Subspace learning is to find subspace models for concise data representation and accurate decision making based on training samples.

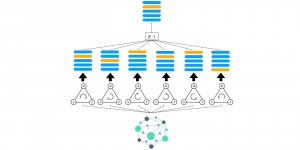
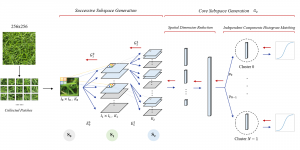
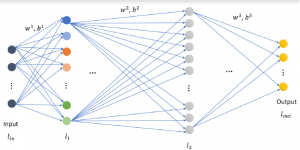
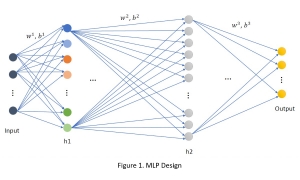
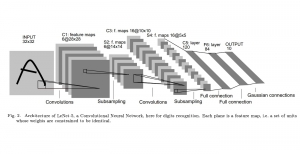
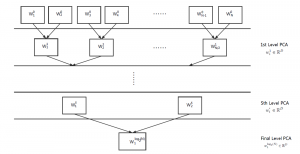
Most existing subspace methods are conducted in a single stage. We may ask whether there is an advantage to perform subspace learning in multiple stages. Research on generalizing from one-stage subspace learning to multi-stage subspace learning is rare. Two PCA stages are cascaded in the PCAnet, which provides an empirical solution to multi-stage subspace learning. Little research on this topic may be attributed to the fact that a straightforward cascade of linear multi-stage subspace methods, which can be expressed as the product of a sequence of matrices, is equivalent to a linear one-stage subspace method. The advantage of linear multi-stage subspace methods may not be obvious from this viewpoint.

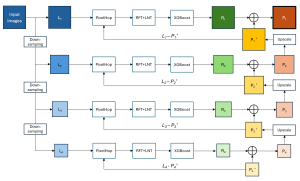
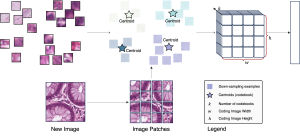
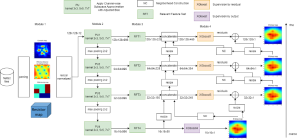
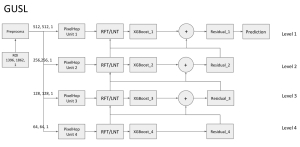
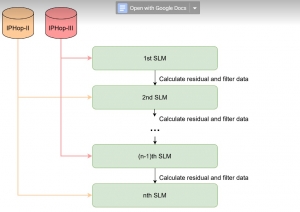
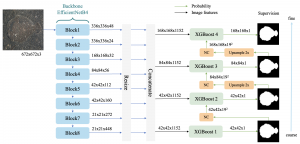
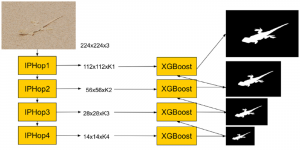
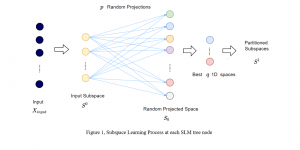
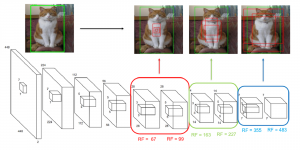
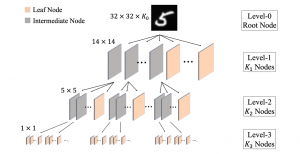
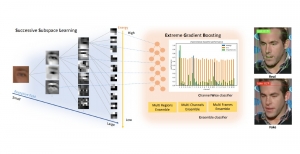
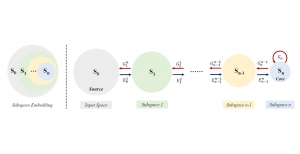
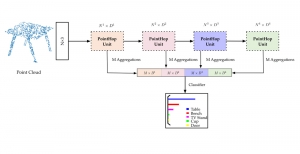
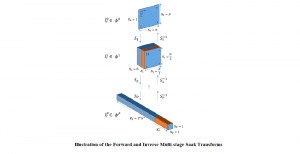
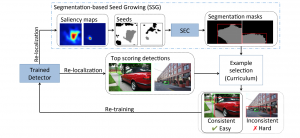
Yet, multi-stage subspace learning may be worthwhile under the following two conditions. First, the input subspace is not fixed but growing from one stage to the other. For example, we can take the union of a pixel and its eight nearest neighbors to form an input space in the first stage. Afterward, we enlarge the neighborhood of the center pixel from 3×3 to 5×5 in the second stage.  Clearly, the first input space is a proper subset of the second input space. By generalizing it to multiple stages, it gives rise to a “successive subspace growing” process. This process exists naturally in the convolutional neural network (CNN) architecture, where the response in a deeper layer has a larger receptive field. In our words, it corresponds to an input of a larger neighborhood. Instead of analyzing these embedded spaces independently, it is advantageous to find a representation of a larger neighborhood using those of its constituent neighborhoods of smaller sizes in computation and storage efficiency. Second, special attention should be paid to the cascade interface of two consecutive stages so that the multi-stage cascade can offer an effective solution.

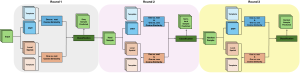
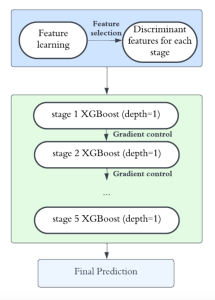
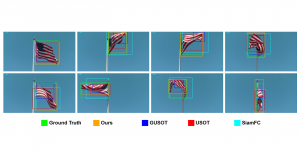
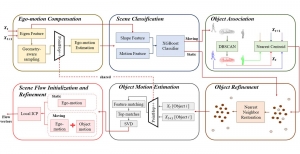
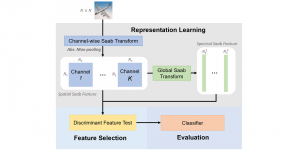
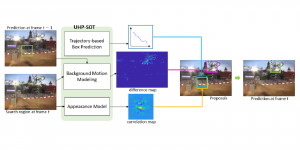
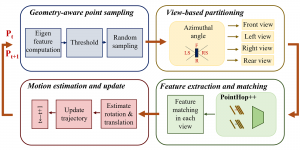
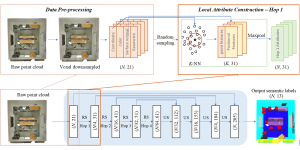
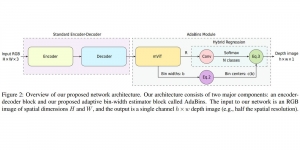
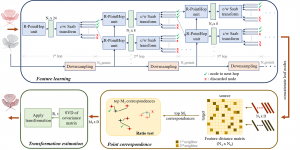
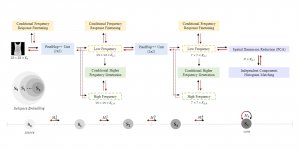
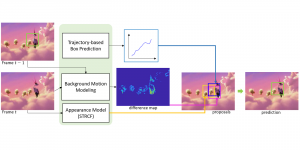
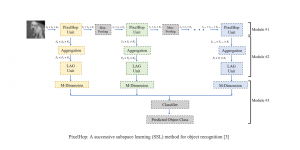
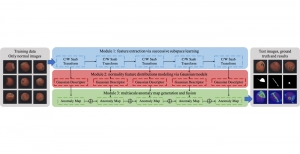
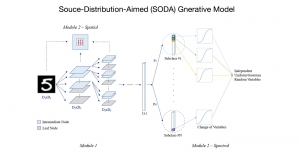
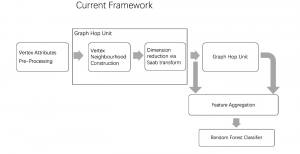
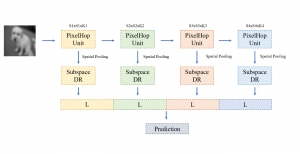
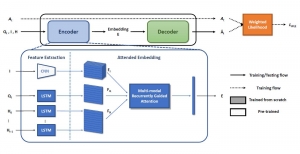
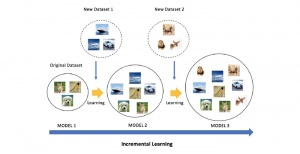
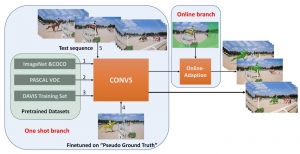
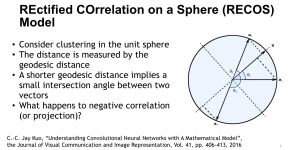
Recently, Professor Kuo and his students at MCL proposed a new machine learning methodology called successive subspace learning (SSL). Although being inspired by the deep learning framework, SSL is fundamentally different in its model formulation, training process and training complexity. Many MCL members are applying SSL to image processing and computer vision problems such as contour detection, image classification, texture analysis, object detection, video object tracking and segmentation, image generation, etc. The research objective is to develop an explainable, robust and effective machine learning methodology that reaches comparable performance offered by deep neural networks.